Entropy Triangle Weka package
A set of information-theoretic tools for the assessment of multi-class classifiers in Weka
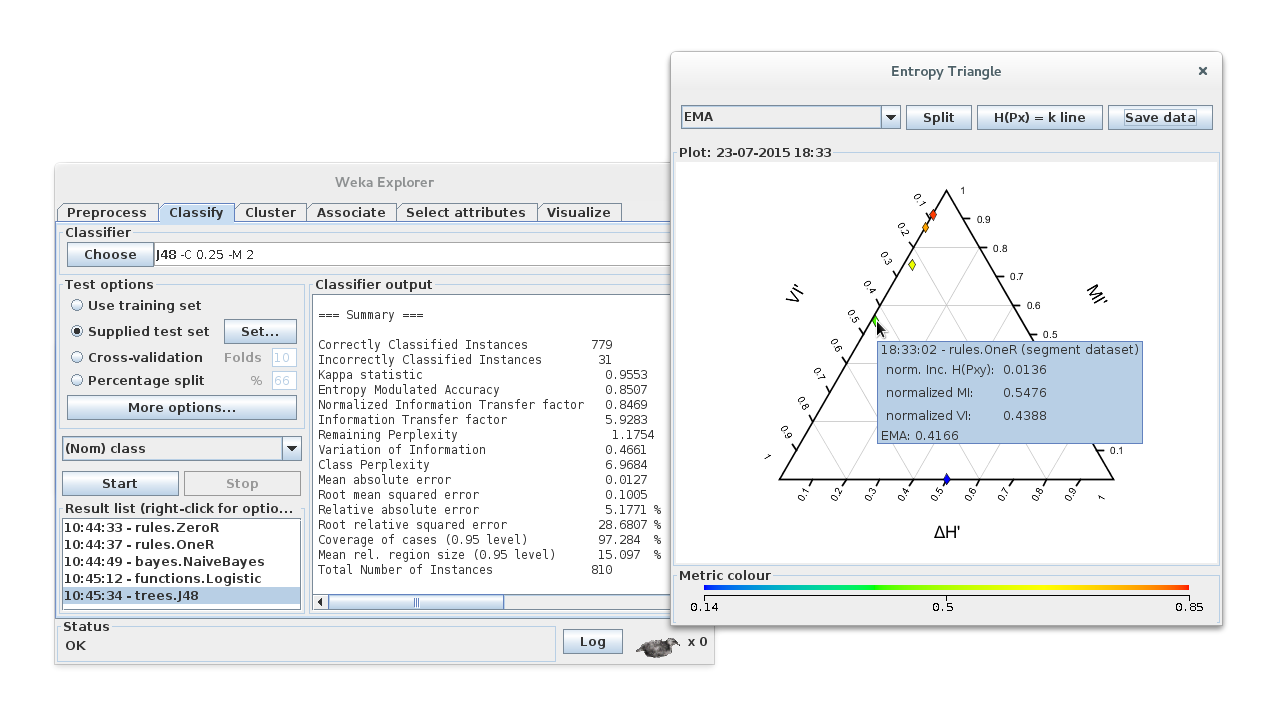
Features
Visualization Plugin with an exploratory data analysis method for an easy, but complete and reliable comparison of classifiers performance.
The Entropy Triangle is based on a balance equation of entropies. Represents normalized values of the variation of information, the mutual information, and the increment of entropy from the uniform distribution in a ternary plot. This lets you analyze at a glance different scenarios without loss of information.
- Panel with colorbar (or labels) for the chosen metric (or classifier/dataset information)
- Tooltips with detailed information hovering graph elements
- Delete elements of the graph with a right-click context menu
- Save and load graph data in arff format
- Export data to csv or json
- Print the graph with Ctrl+Shft+Alt+Left Mouse Click
New evaluation metrics for the standard output of Weka.
Entropy Modulated Accuracy (EMA)
The EMA is a pessimistic estimate of the accuracy with the influence of the input distribution factored out. It is defined mathematically as the inverse of the remaining perplexity after the learning process
$$ EMA = \frac{1}{PP_{X|Y}} = \frac{1}{2^{H_{X|Y}}} $$
Normalized Information Transfer factor (NIT factor).
A measure of how efficient is the transmission of information from the input to the output of the classifier
$$ NIT_{factor} = \frac{\mu_{XY}}{k} $$ where k is the number of classes.
Optional advanced information-theoretic metrics.
Class perplexity
The class perplexity can be interpreted as the number of effective classes at the input of the classifier, due to the likelihood of the input distribution
$$ PP_X = 2^{H_X} $$
Remaining perplexity
The Remaining Perplexity measures the residual difficulty after the learning process $$ PP_{X|Y} = 2^{H_{X|Y}} $$
Information Transfer factor
The Information Transfer factor measures the variation in difficulty due to the mutual information between the input and the output distributions of the classifier. $$ \mu_{XY} = 2^{MI_{XY}} $$
Variation of information $$ VI = H_{X|Y} + H_{Y|X} $$
Theoretical background
This package is an implementation of the work of these papers:
